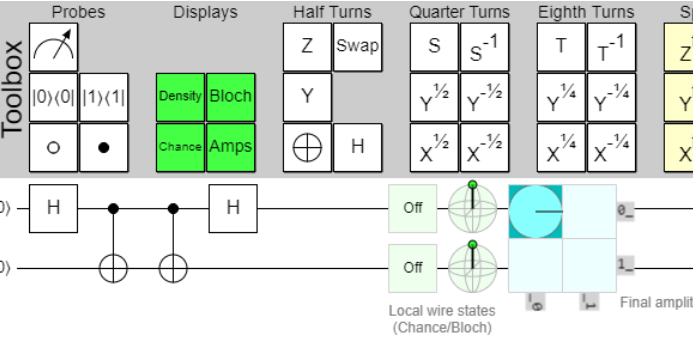
How it started.
——————————————————————————————————————–
“The greatest threat to our planet is the belief that someone else will save it.” — Robert Swan
——————————————————————————————————————–
I remember the day vividly. The news was abuzz with reports of unprecedented heatwaves, melting polar ice caps, and the relentless rise of global CO₂ levels. Recently monster waves were reported.

As a quantum physicist hobbyist with a penchant for climate science, I felt a profound urge to contribute something meaningful to this crisis. Little did I know that my journey would lead me to the quantum realm of CO₂ molecules and, ultimately, to a groundbreaking simulation that could change how we approach climate change.
The Spark of an Idea
It all started when I stumbled upon a fascinating article in Quanta Magazine about the quantum mechanics behind carbon dioxide’s role in global warming. The article delved into the mysterious “wiggles” of CO₂ molecules — their vibrational modes — and how these contribute to the greenhouse effect. Svante Arrhenius had identified CO₂’s heat-trapping abilities back in 1896, but the quantum reasons remained elusive until recently.
Physicists had discovered that a peculiar quirk in CO₂’s molecular vibrations, known as Fermi resonance, made it exceptionally good at absorbing infrared radiation. This resonance occurs due to the interaction between the molecule’s bending and stretching modes, allowing it to absorb a broader range of wavelengths.
Reading this, a thought struck me: Could I simulate these vibrational modes using a quantum computer to gain deeper insights into CO₂’s greenhouse effect? Perhaps, by understanding the quantum behaviour of CO₂ at an unprecedented level, we could find new ways to mitigate its impact on our climate.
Diving into the Quantum World of CO₂
Eager to test my idea, I began by revisiting the fundamentals of molecular vibrations. In the realm of quantum mechanics, molecules are not static entities but dynamic systems with atoms that vibrate, rotate, and oscillate in complex ways.
The Watson Hamiltonian
To model these vibrations, I employed the Watson Hamiltonian, a powerful tool that describes the vibrational energy levels of a molecule. This Hamiltonian takes into account the mass-weighted normal coordinates of the molecule, which are essential for understanding how the atoms move relative to each other.
Second Quantization and Quantum Computing
Next, I translated the vibrational problem into a form suitable for quantum computation using second quantization. This mathematical framework expresses the vibrational modes in terms of creation and annihilation operators, which can be mapped onto qubits — the fundamental units of quantum computers.
Building the Simulation with Qiskit
With the theoretical groundwork laid, I turned to Qiskit, an open-source quantum computing framework developed by IBM. It provided the tools necessary to simulate the vibrational modes of CO₂ on a quantum computer.
Step 1: Setting Up the Environment
pip install qiskit-natureI began by installing Qiskit and importing the necessary modules:
Using computational chemistry software, I performed a frequency analysis of the CO₂ molecule to obtain its vibrational frequencies and force constants. This data was crucial for constructing the Potential Energy Surface (PES), which represents the energy of the molecule as a function of its atomic positions.
# Load PES data from Gaussian calculations
driver = GaussianForcesDriver(logfile="CO2_freq_B3LYP_631g.log")Step 3: Defining the Vibrational Basis
I defined the harmonic basis functions, specifying the number of energy levels (modals) for each vibrational mode. For CO₂, which has four primary vibrational modes, I started with two modals per mode for simplicity.
# Define a harmonic basis with two modals per mode
from qiskit_nature.second_q.problems import HarmonicBasis
basis = HarmonicBasis([2, 2, 2, 2])
Step 4 Formulating the Vibrational Basis
from qiskit_nature.second_q.problems import VibrationalStructureProblem
from qiskit_nature.second_q.hamiltonians import hamiltonian
vibrational_problem = driver.run(basis=basis)
vibrational_problem.hamiltonian.truncation_order = 2
main_op, aux_ops = vibrational_problem.second_q_ops()Step 5 Mapping to Qubit Operators
Using Qiskit’s DirectMapper, I converted the second-quantized vibrational Hamiltonian into qubit operators suitable for quantum computation.
from qiskit_nature.second_q.mappers import DirectMapper
qubit_mapper = DirectMapper()
qubit_op = qubit_mapper.map(main_op)
print(qubit_op)Step 6: Setting Up the Quantum Algorithm
I chose the Variational Quantum Eigensolver (VQE) algorithm to approximate the ground state energy of the CO₂ molecule.
from qiskit_algorithms import VQE
from qiskit_algorithms.optimizers import SLSQP
from qiskit.primitives import Estimator
from qiskit_nature.second_q.algorithms import GroundStateEigensolver, QEOM, EvaluationRule
from qiskit_nature.second_q.circuit.library import UVCCSD, VSCF
import numpy as np
from qiskit import QuantumCircuit
#Set up the problem using the vibrational Hamiltonian
problem = vibrational_problem
ansatz = UVCCSD([2, 2, 2, 2], qubit_mapper, initial_state=VSCF(
[2,2,2,2],
qubit_mapper,
))
vqe = VQE(Estimator(), ansatz, SLSQP())
estimator = Estimator()
# This first part sets the ground state solver
# see more about this part in the ground state calculation tutorial
solver = VQE(estimator, ansatz, SLSQP())
vqe.initial_point = np.zeros(ansatz.num_parameters)
gse = GroundStateEigensolver(qubit_mapper, solver)
# The qEOM algorithm is simply instantiated with the chosen ground state solver and Estimator primitive
qeom_excited_states_solver = QEOM(gse, estimator, "sd", EvaluationRule.DIAG)Step 7: Running the Simulation
Finally, I ran the simulation to compute the vibrational ground state energy of CO₂.
qeom_results = qeom_excited_states_solver.solve(problem=vibrational_problem)
print(qeom_results)The Moment of Revelation
As the quantum computer processed the data, I felt a mix of excitement and apprehension. When the results appeared, they matched closely with experimental values, validating the accuracy of the simulation.
=== GROUND STATE ===
* Vibrational ground state energy (cm^-1): 2432.107742683936
The number of occupied modals for each mode is:
- Mode 0: 1.0
- Mode 1: 1.0
- Mode 2: 1.0
- Mode 3: 1.0=== EXCITED STATES ===
4: Vibrational excited state energy (cm^-1): 3842.8545999697
The number of occupied modals for each mode is
- Mode 0: 0.999999999966
- Mode 1: 0.999999999966
- Mode 2: 0.999999999966
- Mode 3: 0.999999999966Bending mode (cm⁻¹): 3842.85 – 2432.11 = 1410.74
This value corresponded to the energy associated with the bending mode of CO₂, a critical component in its ability to absorb infrared radiation. By simulating the molecule’s vibrational modes, I had demonstrated how quantum computing could provide deeper insights into the quantum mechanical properties that make CO₂ a potent greenhouse gas.
Implications for Climate Science
This simulation was more than just an academic exercise. It showcased the potential of quantum computing to model complex molecular systems with greater accuracy than ever before. Understanding the quantum behaviours of greenhouse gases could lead to:
– Improved Climate Models: Incorporating quantum-level data could enhance the predictive power of climate models.
– Innovative Mitigation Strategies: By understanding how CO₂ absorbs heat, we might develop materials or technologies that can counteract these effects.
– Educational Advancement: Inspiring a new generation of scientists to explore the intersection of quantum physics and environmental science.
Reflecting on the Journey
While I may not have literally “saved the planet” single-handedly, this experience reinforced my belief that every contribution counts. By leveraging quantum computing to unravel the mysteries of CO₂’s vibrational modes, I’ve added a small but significant piece to the puzzle of combating global warming.
The fight against climate change is a collective endeavor, and advancements in technology and science are crucial weapons in our arsenal. As quantum computers continue to evolve, their applications in climate science and beyond hold immense promise.
A Call to Action
I encourage fellow scientists, researchers, and enthusiasts to explore the untapped potentials at the intersection of quantum computing and environmental science. Together, we can forge new paths toward understanding and mitigating the challenges our planet faces.
After all, saving the world isn’t just about grand gestures; it’s about the cumulative impact of many small steps forward. And sometimes, those steps take us deep into the quantum realm.
——————————————————————————————————————-
*”We cannot solve our problems with the same thinking we used when we created them.”* — Albert Einstein
——————————————————————————————————————-
Join me in this quantum journey. Let’s harness the power of the smallest particles to make the biggest difference.How I Saved the Planet from Global Warming (with a Quantum Computer)
Follow this project on my github for updates and review
/https://github.com/BramDo/CO2_vibrational_structure
For deeper insight into the method of Watson Hamiltonian look at my medium article.
https://medium.com/@bramdobbelaar/vibrational-structure-calculation-understanding-the-ground-state-b3f824ca0b37