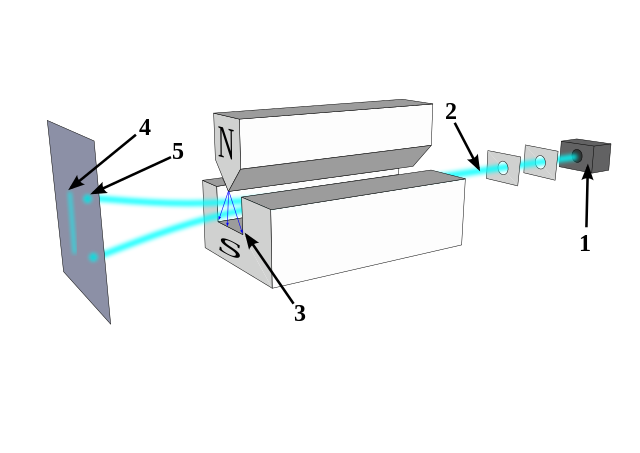
1. Introduction to the Experiment
- The Delayed Choice Quantum Eraser Experiment was first proposed by physicists Scully and Drühl in 1982 and was experimentally demonstrated in 1999 by researchers at the University of Maryland.
- The goal of this experiment was to explore the dual nature of photons (or other quantum particles), showing how they can behave either like particles or waves depending on the availability of information about their path.
- This experiment builds on the classic double-slit experiment, where photons (or electrons) create an interference pattern on a screen, which is indicative of their wave-like nature. However, if you know which slit the photon passed through (i.e., particle behavior), the interference pattern disappears.
2. Basic Setup of the Delayed Choice Quantum Eraser
Double-Slit Experiment
- At its core, the setup involves a variation of the double-slit experiment:
- A source emits individual photons that pass through two slits.
- These photons, if left undisturbed, create an interference pattern on the screen, which is the result of their wave-like behavior.
Introducing Entanglement
- To make the setup more interesting, instead of allowing the photons to freely interfere, a Beta Barium Borate (BBO) Crystal is introduced.
- This crystal generates entangled photon pairs via a process called spontaneous parametric down-conversion.
- One photon, known as the screen photon, continues toward the screen (just as in the classic double-slit experiment).
- The second photon, called the information photon, is sent in another direction and holds “which-path” information about which slit the original photon passed through.
Which-Path Information
- The information photon contains data about the specific slit (top or bottom) the screen photon went through.
- The entangled state means that the behavior of the screen photon is linked to the information photon.
3. Common Misconceptions
- One common misunderstanding about this experiment is that if we don’t measure the information photon, the interference pattern will appear on the screen. But if we do measure it, the interference pattern will be destroyed.
- The video clarifies that this idea is wrong. The moment the two photons become entangled, their behavior changes in such a way that no interference can occur, regardless of whether the which-path information is measured or not.
Decoherence Explained
- Once the photons are entangled, they are part of a global wave function.
- This global wave function cannot interfere with itself in the same way that an individual photon could.
- The two photons now exist in separate branches of the wave function, as if they are in different “universes.” Therefore, the screen photon no longer behaves like a wave that can interfere with itself. This is a process called decoherence.
Key Clarification
- No interference will appear on the screen simply because the photons are entangled—the experiment does not require the measurement of the information photon to destroy the interference.
4. Introducing the Quantum Eraser
How It Works
- To scramble or “erase” the which-path information, the experiment adds several mirrors and beam splitters into the path of the information photon.
- These beam splitters work by either transmitting or reflecting the photon with a 50% probability.
- For example, a photon passing through the top slit has a 50% chance of going to detector D1 and a 50% chance of going to detector D2. The same applies to photons passing through the bottom slit.
The Key Idea
- This arrangement scrambles the which-path information. In other words, after the photon passes through the beam splitter, you can no longer be certain whether it came from the top slit or the bottom slit. It could have taken either path with equal probability.
False Claim about Interference
- A common claim is that this “scrambling” of the which-path information should cause the interference pattern to reappear on the screen.
- However, the video once again emphasizes that no interference pattern will appear on the screen, no matter what is done to the information photon.
- This is because the entangled photons still remain part of a global wave function, which prevents them from behaving as independent waves that can interfere with each other.
5. The True Outcome of the Quantum Eraser
Correlated Patterns
- While no interference pattern is observed directly on the screen, the data reveals something fascinating.
- If you selectively look at the screen hits correlated with detections at D1 (or D2), you will see what looks like an interference pattern.
- The photons detected at D1 form one set of bands, while those at D2 form a complementary set of bands.
Why This Happens
- This occurs because the beam splitter introduces different phase shifts in the probability waves reaching D1 and D2.
- As a result, the interference appears in a complementary way: photons associated with D1 will exhibit one pattern, while those associated with D2 will show another.
- This shows that what the beam splitter really does is act like an interferometer, combining the probability waves and causing constructive and destructive interference depending on where the screen photon landed.
6. Conclusion: No Retrocausality
- The final point is that there is no backwards-in-time communication or retrocausality happening in this experiment.
- The patterns observed at the screen are not a result of information traveling backward in time to alter the photon’s behavior after it has hit the screen.
- Instead, quantum mechanics explains the outcomes without invoking any such phenomenon.
The Role of Entanglement
- The entanglement between the screen photon and the information photon ensures that the behavior of the photons is determined by the global wave function, which behaves according to well-understood principles of quantum mechanics.
- When the which-path information is “erased,” it doesn’t change the past but simply affects how we interpret the measurement outcomes.
7. Recap
- Sum up
- The wave function of the photons is described mathematically, and the probability density for where photons will land on the screen is derived.
- These equations demonstrate that quantum mechanics predicts the results of the experiment without the need for retrocausality.
- The superposition of wave functions and the resulting interference between probability waves explains the data.
Thats it
This detailed breakdown from the introduction of the concept to the final debunking of popular misconceptions, could help the reader the Delayed Choice Quantum Eraser Experiment.
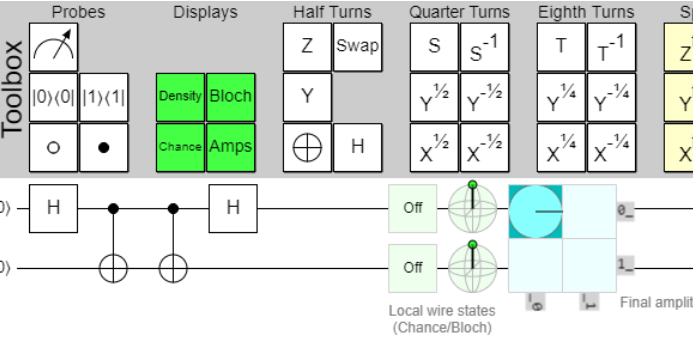
Lets do some quantum simualtion in python
import numpy as np
# Define basic quantum states
ket_0 = np.array([[1], [0]]) # |0> state
ket_1 = np.array([[0], [1]]) # |1> state
# Pauli-X gate (quantum NOT gate)
X_gate = np.array([[0, 1], [1, 0]])
# Hadamard gate to create superposition
H_gate = (1 / np.sqrt(2)) * np.array([[1, 1], [1, -1]])
# Define projection operators for measurement
proj_0 = np.dot(ket_0, ket_0.T)
proj_1 = np.dot(ket_1, ket_1.T)
# Function to entangle signal and idler photons
def entangle(signal, idler):
# Combine signal and idler into a 4-element vector (tensor product)
combined_state = np.kron(signal, idler)
# Create entanglement using CNOT gate
CNOT = np.array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 0, 1],
[0, 0, 1, 0]])
entangled_state = np.dot(CNOT, combined_state)
return entangled_state
# Initial photon state: superposition of |0> and |1>
initial_photon = np.dot(H_gate, ket_0)
initial_idler = ket_0
# Entangle the signal and idler photons
entangled_state = entangle(initial_photon, initial_idler)
# Simulate which-path measurement on the signal photon
# We measure the signal photon in the computational basis
measure_0 = np.kron(proj_0, np.identity(2))
measure_1 = np.kron(proj_1, np.identity(2))
# Probabilities of outcomes
prob_0 = np.abs(np.dot(measure_0, entangled_state).T @ np.dot(measure_0, entangled_state))
prob_1 = np.abs(np.dot(measure_1, entangled_state).T @ np.dot(measure_1, entangled_state))
# Normalize the post-measurement states
state_after_measurement_0 = np.dot(measure_0, entangled_state) / np.sqrt(prob_0)
state_after_measurement_1 = np.dot(measure_1, entangled_state) / np.sqrt(prob_1)
# Now, apply Hadamard gate to the idler photon to erase which-path information
H2 = np.kron(np.identity(2), H_gate)
erased_state_0 = np.dot(H2, state_after_measurement_0)
erased_state_1 = np.dot(H2, state_after_measurement_1)
# Display the results
print("Entangled State (Signal and Idler Photons):\n", entangled_state)
print("\nState After Measurement (Outcome |0>):\n", state_after_measurement_0)
print("\nState After Measurement (Outcome |1>):\n", state_after_measurement_1)
print("\nErased State After Applying Hadamard to Idler (Outcome |0>):\n", erased_state_0)
print("\nErased State After Applying Hadamard to Idler (Outcome |1>):\n", erased_state_1)
Entangled State (Signal and Idler Photons):
[[0.70710678]
[0. ]
[0. ]
[0.70710678]]
State After Measurement (Outcome |0>):
[[1.]
[0.]
[0.]
[0.]]
State After Measurement (Outcome |1>):
[[0.]
[0.]
[0.]
[1.]]
Erased State After Applying Hadamard to Idler (Outcome |0>):
[[0.70710678]
[0.70710678]
[0. ]
[0. ]]
Erased State After Applying Hadamard to Idler (Outcome |1>):
[[ 0. ]
[ 0. ]
[ 0.70710678]
[-0.70710678]]
his output shows the states at each significant step in the simulation:
- Entangled State: The initial entangled state of the signal and idler photons.
- State After Measurement: The state of the system after measuring the signal photon in the computational basis for both possible outcomes (∣0⟩|0\rangle∣0⟩ and ∣1⟩|1\rangle∣1⟩).
- Erased State After Applying Hadamard to Idler: The state after applying the Hadamard gate to the idler photon, effectively “erasing” the which-path information.
This demonstrates how the interference pattern can be restored by manipulating the idler photon after a measurement has been made on the signal photon.