The molecular Hamiltonian, which governs the behavior of molecules, can be simplified using the Born-Oppenheimer approximation. This approximation is crucial because it decouples the movement of nuclei and electrons due to their vast difference in mass, allowing us to treat these components separately.
For vibrational structure calculations, we first solve the electronic Schrödinger equation to obtain the electronic energy for various geometries of the molecule. This data is used to generate the potential energy surface (PES), which serves as the foundation for solving the nuclear Schrödinger equation. This equation describes the vibrational and rotational behavior of the nuclei in a molecule.
The nuclear Schrödinger equation can be tackled in two primary steps:
- Single-particle basis functions, called modals, are determined either through the harmonic approximation of the PES or by more sophisticated techniques like the Vibrational Self-Consistent Field (VSCF) method.
- Anharmonic effects (non-harmonic behavior) are incorporated using perturbative or variational methods, such as Vibrational Configuration Interaction (VCI) or Vibrational Coupled Cluster (VCC) approaches. These methods are accurate but computationally expensive, limiting their application to small molecules.
Vibrational Ground State and the Watson Hamiltonian
For vibrational ground state calculations, we start by considering the Watson Hamiltonian, a form of the nuclear Hamiltonian that focuses on vibrational modes, neglecting rotational-vibrational coupling. This Hamiltonian uses mass-weighted normal coordinates to describe molecular vibrations.
The vibrational Hamiltonian, denoted Hvib, is defined as
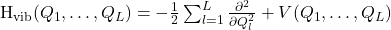
in which
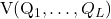
is the potential energy as a function of these coordinates.
For vibrational ground state computations, the main goal is to find the lowest eigenvalue of this Hamiltonian, corresponding to the ground state energy.
Second Quantization and Qiskit
In the context of quantum computing, vibrational structure calculations can be mapped to a qubit-based system using second quantization. This involves:
- Expressing the vibrational Hamiltonian in terms of creation and annihilation operators for each vibrational mode.
- Mapping these operators to qubit-based systems using techniques such as the DirectMapper in Qiskit, a quantum computing framework.
By representing the vibrational problem in this way, we can simulate it on quantum hardware. Qiskit offers tools to perform this mapping, allowing for the approximation of the PES using a quartic force field. This step is essential for incorporating anharmonicity in the vibrational analysis.
Introduction to Molecular Vibrational Structure
The Born-Oppenheimer approximation simplifies molecular Hamiltonians by decoupling the motion of electrons and nuclei. This separation enables us to treat the nuclear motion independently from the electronic structure. The molecular wavefunction is therefore factored into two components:
- Electronic wavefunction, which is derived from solving the electronic Schrödinger equation for a fixed nuclear geometry.
- Vibro-rotational wavefunction, which describes the nuclear motion on the potential energy surface (PES) created by the electronic energy at different nuclear configurations.
To compute the vibrational structure, the nuclear Schrödinger equation is solved within this PES. The process is typically divided into two main steps:
- Single-particle basis (modals): These are either approximated by harmonic oscillators or derived through Vibrational Self-Consistent Field (VSCF) methods, which optimize the vibrational wavefunctions self-consistently.
- Anharmonic Corrections: As real molecular vibrations deviate from simple harmonic behavior, anharmonic effects are incorporated using methods like VCI or VCC.
Vibrational Configuration Interaction (VCI) and Vibrational Coupled Cluster (VCC)
Vibrational Configuration Interaction (VCI)
The VCI method is an extension of the standard configuration interaction (CI) approach used in electronic structure calculations, adapted to the vibrational problem. In this approach:
- The vibrational wavefunction is expanded as a linear combination of vibrational configurations, which are generated by exciting one or more vibrational modes from their reference (ground state) configuration.
- The Hamiltonian matrix is then constructed using these vibrational configurations and diagonalized to obtain the vibrational energy levels.
VCI is particularly useful because it can systematically improve the accuracy of vibrational energies by including higher-order excitations (e.g., single, double, triple excitations) until convergence is achieved. However, the scaling of this method becomes prohibitive for large molecules, as the number of configurations grows exponentially with system size. This restricts VCI applications to smaller molecules, typically with fewer than 10 atoms.
In summary, VCI provides a highly accurate solution for vibrational ground and excited states but suffers from unfavorable computational scaling as the molecule’s size increases.
Vibrational Coupled Cluster (VCC)
The Vibrational Coupled Cluster (VCC) method is another variational approach that builds upon the coupled cluster method commonly used in electronic structure theory. VCC includes:
- Exponentially parametrized wavefunctions, where the wavefunction is written as ∣Ψ⟩=eT∣Φ0⟩|\Psi\rangle = e^{T} |\Phi_0\rangle∣Ψ⟩=eT∣Φ0⟩, with TTT being a cluster operator that excites vibrational modes from the reference state ∣Φ0⟩|\Phi_0\rangle∣Φ0⟩.
- Like VCI, VCC also accounts for anharmonic effects by considering excitations of multiple vibrational modes. However, the cluster operator in VCC can include higher-order terms, and the method’s non-linear nature offers better convergence for highly correlated vibrational problems.
The main advantage of VCC over perturbative methods is its ability to handle strong anharmonic couplings between different vibrational modes. Similar to VCI, the method’s accuracy can be systematically improved by considering higher-order excitations, but it also faces computational limitations for larger systems due to its steep scaling.
Both VCI and VCC are ideal for highly accurate vibrational energy calculations in small molecular systems but require significant computational resources. Their practical application is usually limited to small molecules due to their exponential scaling with the number of vibrational modes.
The Watson Hamiltonian and Vibrational Ground State Calculation
The Watson Hamiltonian, which neglects rotational-vibrational coupling, is often used for vibrational calculations. It operates in mass-weighted normal coordinates and takes the following form:
The ground state corresponds to the lowest eigenvalue of this Hamiltonian, representing the system’s lowest energy vibrational state.
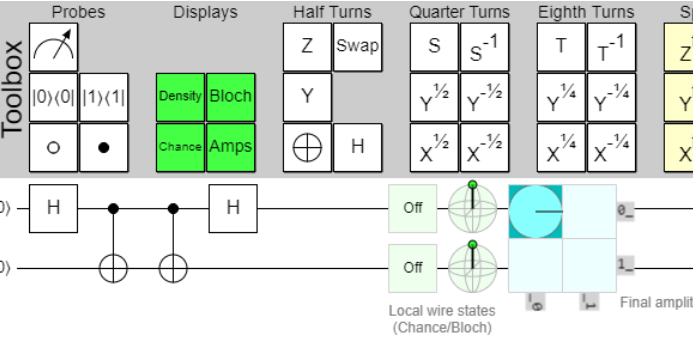
To encode this Hamiltonian for quantum simulations, it needs to be mapped to qubit-based systems using second quantization methods.
Second Quantization and Quantum Computation with Qiskit
In quantum computing, vibrational calculations involve expressing the vibrational Hamiltonian in second quantization. This process includes:
- Expanding the potential energy V(Q1,…,QL)V(Q_1, \dots, Q_L)V(Q1,…,QL) as a Taylor series around the equilibrium geometry, often up to the quartic level for anharmonic systems. The potential energy function is then expressed in terms of vibrational modes using second quantization operators (creation and annihilation operators).
- Mapping to qubit operators: The second quantization operators, which represent vibrational modes, are mapped to qubits using techniques such as the DirectMapper provided by Qiskit. This allows the vibrational structure problem to be solved on quantum hardware.