tekst
\(\)
How to write a mathematical description of a LCU qubisation embedded in
a QPE algorithm.
1. A Hermetian operator $H$ is written as a linear combination of unitaries.
$$H =\ \sum_{i=0}^{L-1} \,\omega_i\,U_i,$$
where Ua are unitary matrices with coefficents. The one-norm of the LCU,
$$\lambda =\sum_{i=0}|\omega_i|$$
For a one‐qubit toy model we take
$$U_0 = I,\qquad U_1 = X,\qquad U_2 = Z,
\quad
H = 1.5\,I + 0.5\,X – 0.5\,Z .
$$
2. Normalisation Factor
$$\lambda =\sum_{i=0}^{L-1}|\omega_i|
=\ 1.5 + 0.5 + 0.5 =\ 2.5 .
$$
Hence
$$\frac{H}{\lambda}
=\sum_{i=0}^{L-1}
\frac{|\omega_i|}{\lambda},
s_i\,U_i,$$
3. Ancilla Preparation PREP
Let $m=\lceil\log_2 L\rceil$ (here $m=2$).
Prepare
$$|\chi\rangle=
\sum_{i=0}^{L-1}
\sqrt{\tfrac{|\omega_i|}{\lambda}}
|i\rangle
=\
\sqrt{0.6}\|00\rangle
+\sqrt{0.2}\|01\rangle
+\sqrt{0.2}\|10\rangle,
$$
via a unitary
$$PREP:\
|0^{\otimes m}\rangle\!\mapsto|\chi\rangle .$$
4. SELECT
$$SELECT
=\sum_{i=0}^{L-1}\|i\rangle\langle i|\otimes s_i\,U_i
=\
|00\rangle\langle00|\otimes I
+\
|01\rangle\!\langle01|\otimes X
+\
|10\rangle\!\langle10|\otimes(-Z).
$$
5. Block‐Encoding Unitary
$$U
=\
(PREP^\dagger\otimes I)
SELECT
(PREP\otimes I).
$$
Projecting the ancilla onto
$|0^{\otimes m}\rangle$ returns
$$\bigl(\langle0^{\otimes m}|\otimes I\bigr)\,
U\,
\bigl(|0^{\otimes m}\rangle\otimes I\bigr)
\;=\;
\frac{H}{\lambda}.
$$
6. Walk Operator (Qubitisation)
Define the reflection
$$R = 2|0^{\otimes m}\rangle\!\langle0^{\otimes m}| – I_{2^{m}},$$ and
the *walk operator*
$$W= R\,U .$$ For every eigenvector
$|\psi_j\rangle$ of $H$ with eigenvalue $E_j$,
$$W\bigl(|0^{\otimes m}\rangle\otimes|\psi_j\rangle\bigr)
=\
e^{\pm i\theta_j}\,
\bigl(|0^{\otimes m}\rangle\otimes|\psi_j\rangle\bigr),
\qquad
\cos\theta_j = \frac{E_j}{\lambda}.$$
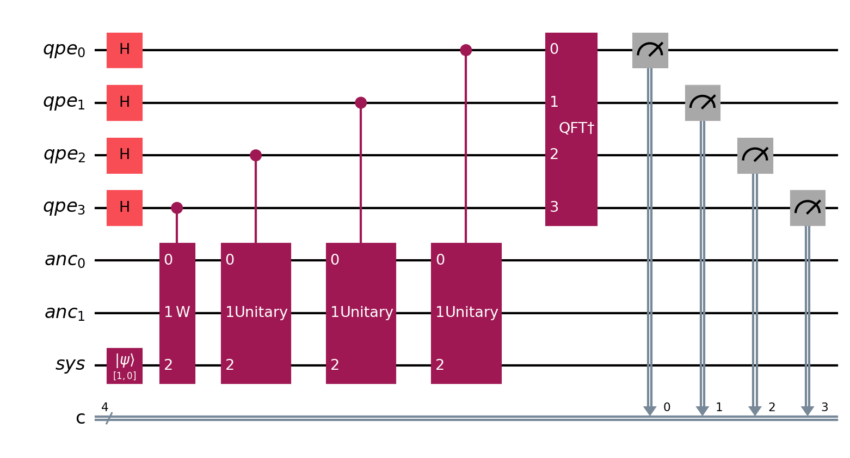
7. Using QPE
Because $W$ is unitary and its phases $\theta_j$ directly encode the
eigen-energies, standard Quantum Phase Estimation on $W$ yields
$$E_j = \lambda\,\cos\theta_j .$$
8. Walkoperator in QPE
The walk operator is the essential bridge between a block-encoded
Hamiltonian and the phase spectrum required by Quantum Phase Estimation.
Its theoretical justification follows directly from the qubitisation
results in Low & Chuang, *npj Quantum Information* **3**, 13 (2017).
$$\frac{H}{\lambda}=\sum_{i=0}^{L-1},
\frac{|\omega_i|}{\lambda}\;
s_i\,U_i,$$