summary
Quantum computing offers a transformative approach to solving linear equations, with the potential to outperform classical algorithms significantly in specific contexts. Central to this field is the Harrow-Hassidim-Lloyd (HHL) algorithm, a pioneering quantum algorithm that enables the efficient resolution of linear systems of equations of the form ( Ax = b ), where ( A ) is a Hermitian matrix. By leveraging unique quantum properties like superposition and entanglement, the HHL algorithm dramatically reduces the time complexity associated with traditional methods, making it particularly advantageous for large-scale problems in various applications, including machine learning and optimization.[1][2]
The HHL algorithm is foundational in the development of subsequent quantum algorithms for linear systems, such as the Quantum Principal Linear Solver (QPLS). QPLS enhances the efficiency of computations and integrates concepts from quantum machine learning, broadening the range of problems it can address. Notable features of the QPLS include efficient oracle preparation and controlled unitary operations, which improve query complexity and scalability, especially for sparse matrices.[3][4]
However, the implementation of quantum algorithms for linear systems is not without its challenges. The efficiency of initial quantum state preparation, the influence of the matrix’s condition number on query complexity, and issues related to scalability and error rates are significant hurdles that researchers are working to overcome.[1][5]
As advancements in quantum computing continue, addressing these challenges will be crucial for realizing the full potential of quantum linear solvers in practical applications. In summary, while the HHL algorithm and its successors represent significant strides in quantum computing’s approach to linear systems, ongoing research and development are essential to navigate the complexities of implementation and scalability, ensuring these algorithms can be effectively deployed in real-world scenarios.[1][2][5]
Background
Quantum computing has the potential to revolutionize the way linear equations are solved, significantly outperforming classical algorithms in certain scenarios. The cornerstone of many quantum linear systems algorithms is the Harrow-Hassidim-Lloyd (HHL) algorithm, which provides an efficient method for solving linear systems of equations, specifically of the form ( Ax = b ), where ( A ) is a Hermitian matrix and ( b ) is a known vector.[1]
The HHL algorithm exploits the properties of quantum mechanics, such as superposition and entanglement, to reduce the time complexity associated with classical methods, making it suitable for large-scale problems[1]
Adiabatic Quantum Computing
One of the notable approaches in quantum linear systems is the use of adiabatic quantum computing (AQC). This method relies on the adiabatic theorem, which states that a system can be transformed from an initial ground state to a final ground state of a Hamiltonian if the transformation is done slowly enough. The adiabatic approach has led to the development of algorithms that implement matrix inversion through adiabatic evolution, as highlighted by various works, including the time-optimal adiabatic method..
Complexity Considerations
The complexity of quantum algorithms for linear systems, such as the HHL algorithm, has been a subject of extensive research. It has been established that the query complexity of these algorithms is inherently linked to the precision required for solutions, particularly due to the necessity of phase estimation in the HHL framework[1]
This complexity can be characterized by lower bounds, emphasizing the need for efficient computational strategies[1]
. The overall aim is to find the minimal complexity required to address a broad class of problem instances, which is critical for advancing the field of quantum computing[1].
Challenges and Future Directions
Despite the advancements in quantum algorithms for solving linear systems, several challenges remain. The implementation of quantum algorithms faces practical limitations, including noise and scalability issues. Nonlinear equations, in particular, present additional complexities that require further research to determine the effectiveness of quantum approaches compared to classical methods[1].
Future work is expected to focus on optimizing these quantum algorithms, exploring new techniques for matrix inversion, and evaluating their applicability in real-world scenario.[1]
HHL Algorithm
The Harrow-Hassidim-Lloyd (HHL) algorithm is a groundbreaking quantum algorithm designed to efficiently solve systems of linear equations. It operates under the premise that, given a Hermitian matrix ( A ) and a vector ( |b\rangle ), the algorithm aims to find the vector ( |x\rangle ) such that ( A|x\rangle = |b\rangle )[3][2]
The HHL algorithm achieves this in logarithmic time, providing a significant improvement over classical methods that typically require polynomial time for similar tasks.
Applications of the HHL Algorithm
The HHL algorithm has a wide range of applications, particularly in quantum machine learning (QML) and optimization problems.
- Machine Learning: The algorithm can be utilized for various tasks, such as clustering and classification, where solving linear equations is fundamental[2].
- Data Analysis: In large datasets, the HHL algorithm can efficiently process and analyze data, providing insights that would be computationally expensive with classical methods[2].
- Optimization Problems: The algorithm enhances the efficiency of finding optimal solutions in diverse applications, particularly those involving gradient descent and ordinary differential equations (ODEs)[3][2].
Core Principles of the HHL Algorithm
The HHL algorithm leverages quantum computing resources to solve linear systems in a way that is fundamentally different from classical approaches.
Initialization
The algorithm begins by preparing the quantum state ( |ψ\rangle ), which encodes the input vector ( |b\rangle ) and the eigenvalues of the matrix ( A )[3][2].
The initialization involves setting up quantum registers that will hold this information.
Quantum Phase Estimation
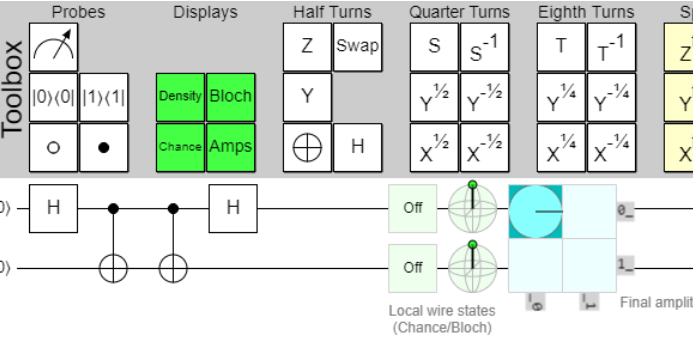
A critical step in the HHL algorithm is Quantum Phase Estimation (QPE), which allows the extraction of the eigenvalues of the matrix ( A ). This is accomplished through a series of controlled operations that manipulate the qubit states based on the eigenvalues, thereby enabling precise measurement of these values. [2][6]
Eigenvalue Inversion
Once the eigenvalues are obtained, the algorithm performs an inversion of these values. This operation is crucial, as it distinguishes the HHL algorithm from classical methods and is essential for obtaining the solution vector ( |x\rangle )[6]
Controlled Rotation and Measurement
Following eigenvalue inversion, controlled rotations are applied to encode the eigenvalues into the quantum state. The final step involves measuring the quantum state to retrieve the solution to the linear system[3][2]. The measurement process is designed to yield a quantum state that represents the solution vector.
Challenges and Future Directions
Despite its potential, the HHL algorithm faces several challenges, including the need for quantum error correction to ensure reliability in practical applications. As quantum computing technology continues to evolve, addressing these challenges will be crucial for the successful implementation of the HHL algorithm in real-world scenarios.[2][6]
Quantum Principal Linear Solver (QPLS)
Overview
The Quantum Principal Linear Solver (QPLS) represents a significant advancement in the field of quantum computing, specifically aimed at solving linear systems of equations. It builds upon foundational work in quantum algorithms, particularly the HHL algorithm, which laid the groundwork for quantum speedups in solving linear systems[1]
QPLS not only enhances the efficiency of these computations but also integrates principles from quantum machine learning, making it applicable to a broader range of problems.
Algorithmic Foundations
The QPLS incorporates several innovative techniques that address the challenges faced in traditional quantum linear system solvers. One such approach is the use of adiabatic quantum computation (AQC), which allows the system to evolve slowly along a path that minimizes excitations. This method enhances the success probability of finding the correct solution by employing a carefully chosen Hamiltonian that governs the dynamics of the quantum system.[7]
Key Features
- Efficient Oracle Preparation: The QPLS utilizes an efficient oracle that operates in polylogarithmic time relative to the size of the input system. This is crucial for scaling up the solution to larger linear systems while maintaining computational efficiency[1].
- Controlled Unitary Operations: The algorithm defines controlled unitary operations that apply transformations to specific registers, allowing for a more structured approach to problem-solving. This capability is essential for ensuring that the eigenstates of the system can be manipulated effectively[7].
- Enhanced Query Complexity: Compared to classical algorithms, the QPLS improves the query complexity, particularly when dealing with sparse matrices and specific conditions such as error rates and condition numbers. This refinement leads to a more robust and efficient algorithm capable of handling a wider variety of linear system problems[1].
Applications
The QPLS finds potential applications in several domains, particularly where linear systems play a crucial role. One of its prominent applications is in the realm of quantum machine learning, specifically in algorithms that require the efficient processing of large datasets through linear transformations, such as Principal Component Analysis (PCA)[4]
. The QPLS also holds promise in solving discretized differential equations, which are prevalent in fields ranging from physics to engineering.
Challenges and Limitations
The implementation of quantum algorithms for solving linear systems, particularly the Harrow-Hassidim-Lloyd (HHL) algorithm and related quantum linear system problem solvers (QLSP), faces various challenges and limitations that affect their practical applicability and efficiency.
Complexity of State Preparation
One of the primary challenges in the HHL algorithm is the efficiency of preparing the initial quantum state. The resources required for state preparation can be significant and, if not managed effectively, may negate the quantum speed-up achieved through the algorithm itself.[1]
. The gate complexity associated with preparing the initial state must be low to ensure that the overall performance remains advantageous compared to classical methods.
Query Complexity and Condition Number
The query complexity of various quantum linear solvers heavily relies on the condition number of the input matrix. A higher condition number indicates that the matrix is close to being singular, which complicates the inversion process and can lead to numerical instability.[1]
. Current algorithms exhibit query complexities that depend on both the condition number and other parameters, creating a bottleneck in achieving optimal performance[1]
. Moreover, while lower bounds for the query complexity have been established, reaching these bounds remains an open question, often requiring new techniques beyond those currently available[1]
Scalability and Implementation Challenges
As quantum hardware continues to advance, the challenge of scalability becomes increasingly relevant. Many quantum algorithms, including those designed for QLSP, struggle with the practical limitations of current quantum systems, such as noise and qubit coherence times.[5]
. Effective implementation of the HHL algorithm demands careful consideration of these factors, particularly when the size of the problem increases. The complexity of maintaining error rates within acceptable limits poses a significant barrier to large-scale applications of these algorithms.
Variational Approaches and Hybrid Architectures
Variational quantum linear solvers (VQLS) represent a promising alternative to traditional quantum algorithms by utilizing a hybrid quantum-classical architecture. However, these approaches introduce their own set of challenges, including the need for classical optimizers and potential convergence issues when minimizing cost functions.[1]While VQLS can be advantageous for specific problem sizes and types, their general applicability and performance relative to other methods remain areas for ongoing research.