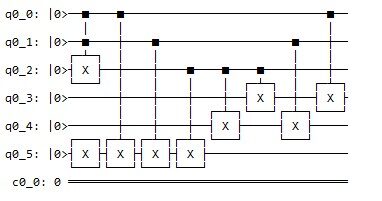
1.1) Openscienceprize find the groundstate of a Heisenberg model.
Why the ground state of a Heisenberg model? Well, the ground state of a system is it’s lowest energy configuration, and the ground state tends to be where exciting and unexpected quantum effects flourish. For example, when the element Mercury is cooled down near its ground state (below 4 Kelvin), it has no electrical resistance. None. Zero! Near its thermal ground state, a chunk of Mercury is a superconductor. Researchers have been trying to understand what materials exhibit superconductivity and how it’s even possible ever since it was first discovered. Kagome lattice is an arrangement of atoms in 2D pattern commonly found in minerals. Figure 1 shows a basic unit cell of the lattice made up of a hexagonal star. Because of its geometry, this lattice is heavily studied in the field of condensed matter physics. When atoms in the lattice are anti-aligned by spin, the triangular shape creates a frustration (right side of figure 1), that is, the atom on the right doesn’t know what to do as it is supposed to be anti-aligned with the one on the left and top at the same time. Figure 1: On the left: Kagome lattice unit cell consisting of 12 vertices. On the right, an example of a frustrated system with atoms anti aligned by spin. This type of frustrated system is believed to be of great importance in the study of spin liquids and superconducting materials at high temperature
1.2) Heisenberg spin-1/2 model on the kagome lattice